Sample code for reducing overfitting problems in deep learning.Answer the following questions:

• How to use dropout to avoid overfitting problem in machine learning?
• How to use regularizer to avoid overfitting problem in machine learning?

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#  create range of monthly dates
download_dates = pd.date_range(start='2019-01-01', end='2020-01-01', freq='MS')
#  URL from Chrome DevTools Console
base_url = ("https://climate.weather.gc.ca/climate_data/bulk_data_e.html?format=csv&"
              "stationID=51442&Year={}&Month={}&Day=7&timeframe=1&submit=Download+Data") #  add format option to year and month
#  create list of remote URL from base URL
list_of_url = [base_url.format(date.year, date.month) for date in download_dates]
#  download and combine multiple files into one DataFrame
df = pd.concat((pd.read_csv(url) for url in list_of_url))
data = df.loc[:, (df != df.iloc[0]).any()]
data=data[data.columns[data.isnull().mean() < 0.9]]
keepcolumns=['Temp (°C)','Dew Point Temp (°C)', 'Rel Hum (%)','Stn Press (kPa)','Wind Spd (km/h)']
data=data[keepcolumns]
predictors=['Temp (°C)', 'Stn Press (kPa)','Dew Point Temp (°C)','Rel Hum (%)']
predictand=['Wind Spd (km/h)']
X = data[predictors].values
y = data[predictand].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=40)
transformer = StandardScaler().fit(X_train)
X_train_t=transformer.transform(X_train)
X_test_t =transformer.transform(X_test)
ytransformer = StandardScaler().fit(y_train)
y_train_t=ytransformer.transform(y_train)
y_test_t =ytransformer.transform(y_test)

L1 is nothing but the Lasso. The lasso uses shrinkage, it’s procedure encourages simple, sparse models (i.e. models with fewer parameters). L2 is called Ridge. When the issue of multicollinearity occurs, least-squares are unbiased, and variances are large. L2 shrinks the parameters and reduces the model complexity. Both of these parameters are defined at the time of learning the linear regression.

import tensorflow as tf
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from tensorflow.keras import regularizers
input_X0=keras.Input(shape=(2,),name='TasandPs')
X=Dense(32,name='Dense32')(input_X0)
X=Dropout(0.3,name='Dropout_dense32')(X) #for overfitting
X=Dense(16,activation='relu',name='Dense16')(X)
X=Dropout(0.1,name='Dropout_Dense16')(X) #for overfitting
X=Dense(8,activation='relu',name='Dense8')(X)
X=Dropout(0.1,name='Dropout_Dense8')(X) #for overfitting
input_X1=keras.Input(shape=(2,),name='TdandHur')
# combine the 2 subset of input for the next step
X=keras.layers.concatenate([X,input_X1],name='Combined')
X=Dense(16,
    kernel_regularizer=regularizers.L1L2(l1=1e-5, l2=1e-4),  #for overfitting
    bias_regularizer=regularizers.L2(1e-4), #for overfitting
    activity_regularizer=regularizers.L2(1e-5), #for overfitting
    activation='relu',name='Dense16_01')(X)
X=Dropout(0.1,name='Dropout_Dense16_01')(X) #for overfitting
X=Dense(8,
    kernel_regularizer=regularizers.L1L2(l1=1e-5, l2=1e-4), #applies both L1 and L2 regularization penalties
    bias_regularizer=regularizers.L2(1e-4), #for overfitting
    activity_regularizer=regularizers.L2(1e-5), #for overfitting        
    activation='relu',name='Dense8_01')(X) #for overfitting
X=Dropout(0.1,name='Dropout_Dense8_01')(X) #for overfitting
output = Dense(1,
    kernel_regularizer=regularizers.L1L2(l1=1e-5, l2=1e-4), #Regularizer to apply a penalty on the layer's kernel
    bias_regularizer=regularizers.L2(1e-4), #Regularizer to apply a penalty on the layer's bias
    activity_regularizer=regularizers.L2(1e-5), #Regularizer to apply a penalty on the layer's output
    activation='sigmoid',name='Final_Output')(X) 
model = keras.Model(
    inputs = [input_X0,input_X1],
    outputs = output
)
model.summary()

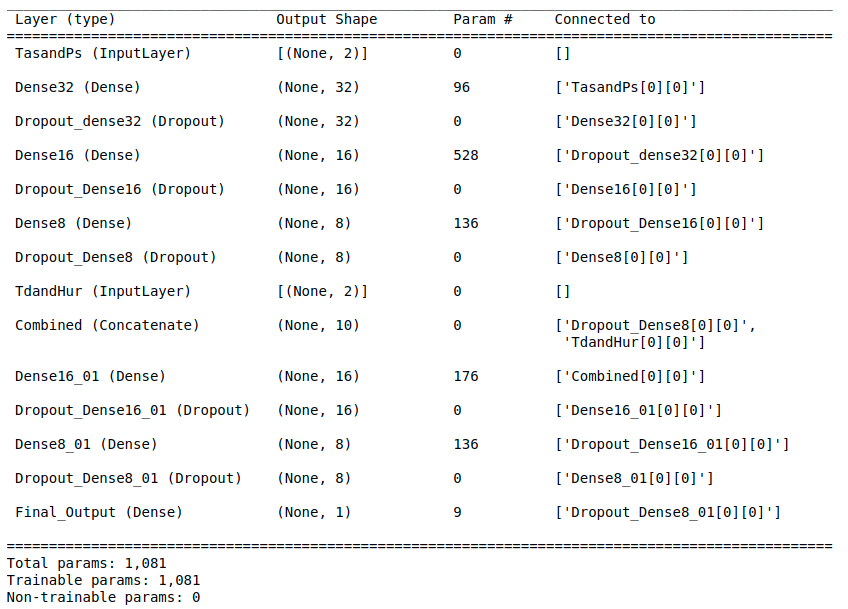
# fit network
model.compile(loss='mae', optimizer='adam')
#model.compile(loss='mse', optimizer='adam')
#model.compile(loss=tf.keras.losses.MeanSquaredLogarithmicError(), optimizer='adam')

history = model.fit(
    {'TasandPs':X_train_t[:,:2],'TdandHur':X_train_t[:,2:]},
    {'Final_Output':y_train_t},
    epochs=10,
    batch_size=64,
    validation_data=({'TasandPs':X_test_t[:,:2],'TdandHur':X_test_t[:,:2]}, {'Final_Output':y_test}),
    verbose=2)
model.save("model_regression1")
keras.utils.plot_model(model, "test.png", show_shapes=True)

from sklearn.metrics import mean_squared_error
pred= model.predict({'TasandPs':X_test_t[:,:2],'TdandHur':X_test_t[:,:2]})
print(np.sqrt(mean_squared_error(y_test_t,pred)))